2. 教学设计
第4讲 数据也有“型”
1.教学内容分析
本节内容首先情境带入,引出数据类型的相关知识内容;随后,以Python编程软件为辅助,讲解整数类型、浮点类型、运算符及Python注释;之后,开展实践任务,以球三角形面积为例,熟悉数据运算符的使用方法;然后,思维拓展,讲解解释器工作原理及注释的作用等知识,最后,能力提升,通过编写Python程序,计算三角形的面积。
2.学习者分析
1.学生具有一定的Python编程语言基础;
2.学生对数据类型有一定的了解;
3.学生具备一定的逻辑推理能力,知识迁移能力,对人工智能的技术有较强的学习兴趣。
3.学习目标确定
1.知识与技能:
①了解 Python 的基本数据类型,掌握整数类型与浮点类型数据的应用方法(整型与浮点型转换);
②了解内置函数 type() 及 pow() 的用法;
③学生能够了解编程规范的一些基本知识。
2.过程与方法:
①通过学习数据类型的相关内容,体会Python编程的应用;
②通过项目的编程练习,培养学生设计能力和举一反三的能力。
3.情感态度与价值观:
①养成自主学习、自主探究的能力;
②培养发现问题、解决问题的探究能力;
③通过对项目的讨论、分析、制作等活动,培养严密的逻辑思维能力。4.教学重点难点
教学重点:1.掌握基本算术运算符的使用方法;
2.了解注释的作用,掌握注释的使用方法;
教学难点:1.掌握整数类型与浮点类型数据的应用方法;
2.灵活运用软件完成项目的制作。
5.教学流程图
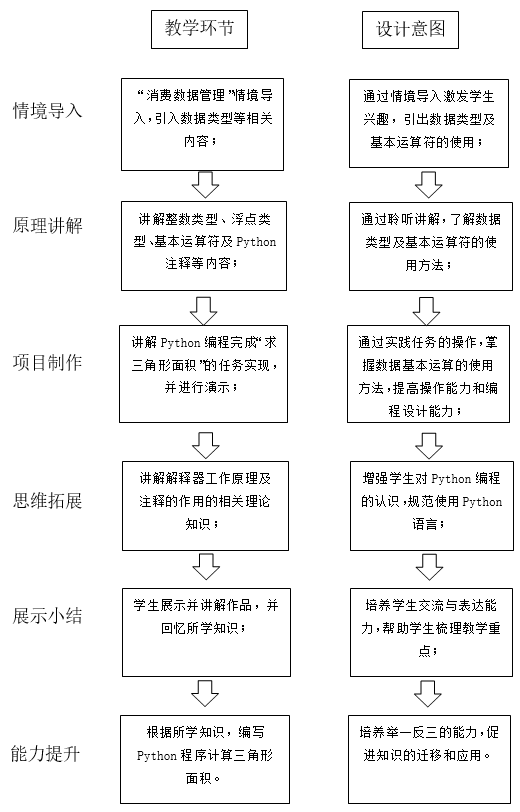
6.教学活动
|
环节一:(情境导入)5min |
|
教学活动1 1.教师讲授情境故事,设置悬念,吸引学生兴趣;(教师播放PPT) 教师:“小楷有自己的零花钱,一般用来买些零食和文具。小楷有个好习惯,就是坚持把零花钱的消费记录在日记本上。如图是某段时间小楷的零花钱消费记录。小楷学了编程之后,就想通过Python程序来管理上述消费记录。比如,算算每月花了多少钱。那么,上面的表格中,除了花费的金额外,日期、地点、购物等信息算不算是要管理的数据?在计算机科学中,数据是指所有能输入到计算机并能被程序所处理的信息。因此,与“花费”一样,“日期”“地点”等信息,都是由数据组成的,只是数据的类型各不相同。那么,如何通过Python编程来管理这些数据呢?消费金额与日期、地点等信息的处理方法是否一样?通过本节开始的学习与体验,大家会了解Python的多种数据类型及其使用方法。” 学生聆听情境故事,积极回应老师,对不同数据类型及使用方法产生兴趣; 教师:“好的,同学们,我们一起去学习一下数据的使用方法吧!今天我们的学习将分成三个模块,第一个模块,学习数据类型的相关知识;第二个模块,一起完成计算求三角形面积的实践任务;第三个模块,思维拓展,解释器工作原理及注释的作用。” 学生聆听教师讲授。 |
|
活动意图说明: 通过情境故事吸引学生的注意力,激发学生的学习兴趣,导入本节课的内容----数据也有“型” |
|
环节二:(原理讲解)20min |
|
教学活动2 1.教师讲解变量数据类型的观察的知识内容,并进行相关演示; 教师:“通过上次课程的学习,我们知道,所有的Python变量都无须提前声明就可以直接赋值,对一个不存在的变量赋值就相当于定义了一个新变量。我们在编程时,往往不去关注变量的数据类型,直接对变量进行赋值和计算,Python中,有一个名为type()的内置函数,可以用来检测某个变量或表达式的当前数据类型。我们可以在交互式编程环境下做些试验,过程如下:其中, int表示整数, float表示浮点型。可以看出, Python变量实际的数据类型是可以发生改变的,同一个变量可以被赋值为整数,可以被赋值为浮点数,也可以被赋值为字符串。也就是说,变量在Python内部是有类型的,比如 int、 fl oat、 str等,我们可以将不同类型的数据赋值给同一个变量。在Python系统中,每个变量在使用前都必须赋值,变量赋值以后该变量才会被创建。根据赋值的情况,变量可以指定成不同的数据类型,可以是整数、小数或字符串。创建变量时解释器会在内存中开辟一个空间。基于变量的数据类型,解释器在分配内存时决定什么数据可以存储其中。所以,人们所说的变量的数据类型是指变量所属内存中所存储数据的类型。我们编写程序时不用去关注变量的数据类型,变量不需要先声明,就可以赋值使用。这也是Python语言简明的地方。接下来做两个编程练习,练习1:数据变量的运算,程序及结果如图;练习2:type函数的使用。程序及结果如图:” 学生认真聆听教师讲解变量数据类型的观察的知识内容,教师播放PPT,进行相关操作演示; 2.教师讲解整数类型的知识内容; 教师:“Python的整数类型与数学中整数的概念一致,也分成正整数和负整数,不带小数点。Python3以上版本中,整数类型理论上的取值范围是[-∞ , +∞ ],也就是说整数类型是没有限制取值范围的,可以当作long类型使用。但实际上由于计算机内存的大小有限,导致整数类型的取值范围受到限制,我们使用的整数是不可能无限大的。Python中内置有一个名为pow(x,y)的函数,用来计算xy的值。利用该函数可以生成一个很大的数。请在交互式编程环境下,利pow(x,y)函数生成一个很大的数,体验一下Python的整数类型的范围。注意:long类型只存在于 Python2.X 版本中,在 Python2.2 以后的版本中,int类型数据溢出后会自动转为long类型。在 Python3.X 版本中long类型被移除,使用int替代。” 学生聆听教师讲解整数类型的知识内容; 3. 教师讲解浮点类型的知识内容,并进行操作演示; 教师:“Python的浮点类型与数学中实数的概念一致,表示带有小数的数值。 Python语言要求所有浮点数必须带有小数部分,小数部分可以是0,这样就区分开浮点类型与整数类型。浮点型由整数部分与小数部分组成,可以用十进制数来表示,如:0.0,3.14159,—2.18,浮点型也可以使用科学计数法来表示。如:2.5e2=2.5×102 = 250。科学计数法使用字母e或E作为幂的符号,以10为基数,含义如下:<a>e<b>= a*10b需要注意的是,浮点类型与整数类型在计算机中的处理方式不同,尽管浮点数0.0与整数0的值相同,但是它们在计算机内部的表示不同。浮点数的数值范围和小数精度也受到计算机系统的限制。接下来,做一个编程练习:练习3: int和float相互转换;程序及结果如图;” 学生聆听教师讲解浮点类型的知识内容,教师播放PPT,进行相关操作演示; 4. 教师讲解基本的算术运算符的知识内容,并进行操作演示; 教师:“Python中,运算符是执行算术等运算的专用符号。其中,用于执行普通数学运算的运算符称为“算术运算符”。通过运算符操作的数值或变量,称为操作数。 Python提供了9个基本的算术运算符,如表4-2所示:以上9个运算符与数学中的计算相对应,运算结果也符合相应数学计算的要求。需要注意的是,算术运算的结果可能会改变操作数变量的数据类型。比如,整数之间的除法,往往计算结果会是浮点数。 Python中,数据类型之间的相互运算所得出的结果允许是“更宽”一点的数据类型,基本规则包括:(1)整数之间运算,如果数学意义上的结果是整数,则最终结果是整数;(2)整数之间运算,如果数学意义上的结果是小数,则最终结果是浮点数;(3)整数与浮点数的混合运算,最终输出的结果是浮点数。以下示例演示了上表中所有Python算术运算符的运算操作情况:结果如图;” 学生认真聆听教师讲解基本的算术运算符的知识内容,教师播放PPT,并进行相关操作演示; 5.教师讲解Python注释知识内容,并进行相关演示; 教师:“注释是编程时在代码中加入的备注信息,可以是续行、单独一行或多行文本,用来对变量、数据结构、语句、函数或计算方法等进行说明,提升代码的可读性。注释是辅助性文本,只是为了提高程序的可读性,不会被计算机编译或解释执行。python语言有两种注释方法:单行注释和多行注释。(1)单行注释python中,单行注释采用 # 开头。例如:以上代码段中,体现出单行注释可以独占一行,也可以放在某语句或表达式的行末。连续的独行单行注释起到了多行注释的效果。(2)多行注释python中,多行注释使用三个单引号(''')或三个双引号(""")开头和结尾。例如,可以使用三个单引号进行注释,如图:这是多行注释,使用连续三个单引号开头,如图;也可以使用三个双引号进行注释:如图,为了程序阅读具有连贯性,程序中的注释一般采用单行注释,标记在关键代码同行。对于一段关键代码,可以在这段代码前采用一个多行注释给出代码的设计原理等说明信息。(3)程序的总体注释规范的程序文件的首行一般都会有一段注释,标记该程序的开发者、修改日期、版本、功能、版权声明等信息。例如图:接下来做一个给Python程序添加注释的编程练习,程序及结果如图;” 学生认真聆听教师讲解Python注释知识内容,教师播放PPT并进行相关演示; |
|
活动意图说明 配合PPT和Python编程语言进行讲解,让学生从亲身经验中体会数据类型及算数运算符的使用方法等知识。 |
|
环节三:(项目制作)25min |
|
教学活动3 教师带领学生借助软件完成求解三角形面积的编程设计; 教师:“生活中,人们常常会遇到三角形面积计算的问题。通常是采用三角形的底边长a乘以高h,再除以2,来计算三角形的面积,计算公式是: S=ah/2。但是在实际工作中,三角形的边长、夹角甚至中线的长度容易测量得准确,高不容易测量准确。因此,生活中往往利用三角形的边长、中线长和夹角度数等易于得到的数值,在不知道高的情况下计算出三角形的面积。本次编程任务要求利用三角形的三边长度,进行面积计算。(1)海伦公式古希腊数学家海伦( Heron,约公元50年)以解决几何测量问题而闻名。在他的著作《度量》一书中,给出了利用三角形的三个边长计算面积的公式,并进行了推导和证明。如果一个三角形的三边长分别为a、b、c,则三角形的面积S为: 其中, P=(a+b+c)/2;(2)如图4-1所示,使用边长进行面积计算的流程可以分为以下三步: 第一步,定义变量a、 b、 c,分别用来存放3个边的边长; 第二步,计算三角形的半周长,即P=(a+b+c)/2; 第三步,最后通过用海伦公式求三角形面积S,即S=sqrt[p(p-a)(p-b)(p-c)];(3)编程实现;利用任意三角形的3个边长测量值,通过海伦公式计算上图中三角形的面积,参考代码及结果如图。” 教师操作Python编程语言,并讲解根据具体操作步骤求解三角形面积的编程设计,并进行操作演示; 学生聆听教师讲解利用Python完成计算三角形面积的编程设计的过程和方法; 教师讲解完成后,教师可留给学生5min时间让学生自己操作学习; |
|
活动意图说明 屏幕共享,教师演示操作,培养学生动手操作能力,让学生直观学习编程设计过程,掌握逻辑结构。 |
|
环节四:(思维拓展)10min |
|
教学活动4 1.教师讲解解释器的工作原理的相关内容; 教师:“编程语言分为编译型语言和解释型语言。 Python是解释型语言,即无须编译,直接能够将源代码解释为机器语言进行运行的语言。这个过程是通过解释器对源代码进行解释执行的。解释器的工作原理如图4-2所示。在Python程序提交执行时,解释器逐一读取源代码,先进行词法分析、语法分析和语义分析,再将源代码转换为解释器能够执行的中间代码(字节码)。最后,由解释器将中间代码解释为可执行的机器指令。也就是说,解释器在语义分析后选择了直接执行语句,这是编译型语言和解释型语言的区别之处,由于解释器的这种工作机制, Python编程时体现出很多灵活性,方便了学习。如:变量不需要指定类型,由解释器执行代码时去辨别数据类型。” 学生认真聆听教师讲解解释器的工作原理的相关内容; 2.教师讲解注释的作用相关内容; 教师:“注释就是对代码的解释和说明,其目的是让人们能够更加轻松地了解代码。注释是编写程序时,写程序的人给一个语句、程序段、函数等的解释或提示,能提高程序代码的可读性。规范的程序注释一般包括序言性注释和功能性注释。序言性注释的主要内容包括模块的接口、数据的描述和模块的功能。模块的功能性注释的主要内容包括程序段的功能、语句的功能和数据的状态。注释的主要用途有:1.标明作者和版权信息。一般每个Python程序文件的首行开始,会添加一段注释,说明程序的作者、修改日期、用途、版权声明等信息。2.解释代码设计的原理、方法及用途。在程序关键语句或程序段处增加注释,解释其原理及作用,增加程序的可读性。3.辅助程序调试。在调试程序时,可以通过单行或多行注释临时屏蔽掉一行或多行程序,使它们不参与程序的执行,辅助程序员定位问题语句的可能位置。” 学生认真聆听教师讲解注释的作用相关内容; 3.教师讲解Python3支持非ASCII码标识符知识内容; 教师:“Python2.x 并不支持包含中文等符号的非 ASCII 码标识符。 2007 年 5 月,名为“Supporting Non-ASCII Identifi ers”的Python增强提案PEP(全称是Python EnhancementProposal) 3131发布,阐述了支持非ASCII码命名标识符的缘由。具体的理由是:很多Python开发者并不熟悉英语,更希望用母语对类、方法等标识符进行命名,而不是用经常有误的英文翻译。对使用同一种母语的开发者来说,用母语命名的标识符可以提高代码清晰度和可维护性。 Python3.x全面支持了非ASCII码标识符, Python 3源码文件以UTF-8编码,所有字符串都是unicode字符串,这样就提高了代码的可读性和可维护性,便于学习和共享交流。” 学生认真聆听教师讲解Python3支持非ASCII码标识符知识内容; |
|
活动意图说明 增强学生对计算机解释器及注释作用的认识,更好利用Python语言进行编程设计。 |
|
环节五:(展示小结)5min |
|
教学活动5 1.学生发言,展示作品,进行逻辑代码讲解; 2.教师对学生作品进行评价; 教师:“同学们,在看了大家的作品后,老师觉得大家都完成的非常好,老师给同学们一个大大的赞。” 总结本节课的知识内容,巩固本节课的知识点,铺垫下一节课。 |
|
环节六:(能力提升)5min |
|
教学活动6 1. 教师讲解三斜求积术原理; 教师:“秦九韶在《数书九章》卷五中写明了问题:“问沙田一段,有三斜(三角形三边),其小斜一十三里,中斜一十四里,大斜一十五里,里法三百步(每300步1里)。欲知为田几何?”“答曰:田积三百一十五顷(每100亩为1顷)。” 秦九韶的三斜求积法,可以表示成与海伦方法相近的计算公式:S=√[(Ma+Mb+Mc)*(Mb+Mc-Ma)*(Mc+Ma-Mb)*(Ma+Mb-Mc)]/3,其中,S为三角形的面积,Ma,Mb,Mc为三角形的中线长度。” 学生聆听教师讲解三斜求积术原理知识内容; 2.根据所学知识,利用Python编程计算三角形面积; 教师:“请利用三角形的3条中线的长度,编写Python程序计算三角形的面积。” |
|
活动意图说明 通过项目式学习的体验效果,让学生可以更直接的体验Python编程的应用,提高学生的参与感。 |
7.板书设计
数据也有“型”
1.数据类型:
整数类型:
浮点类型:
基本算数运算符:
Python注释:
2.三角形面积:8.课后练习与拓展学习设计
请编写Python程序计算三角形面积