一、理论原理
结构方程模型(structural equation modeling,简称SEM),有学者也成称之为潜在变量模型(latent
variable models,LVM)。通常结构方程模型属于多变量统计(multivariate
statistics),它整合了因素分析(factor analysis)与路径分析(path
analysis)两种统计方法,同时检验模型中包含的显性变量、潜在变量、干扰或误差变量间的关系,进而获得自变量对因变量的直接效果、间接效果或总效果。【1】
(一)结构方程模型的类型
结构方程模型基本上是一种验证性的方法,通常必须有理论或经验法则支持,由理论来引导,在理论导引的前提下才能建构假设模型图。即使模型的修正,也必须依据相关理论而来,它特表强调理论的合理性。结构方程模型中有两个基本的模型:测量模型和结构模型。【1】
1. 测量模型
测量模型由潜在变量与观察变量组成。观察变量是量表或问卷等测量工具所得的数据,即各题项所测量的数据;潜在变量是观察变量间所形成的特质或抽象概念,是各题项所抽取的共同因素或概念。观察变量通常以长方形符号表示,潜在变量通常以椭圆符号表示。【1】
在数据分析时,每个观察变量的因子载荷量越高,表示受到潜在变量影响的强度越大;因子载荷量越低,表示受到潜在变量影响的强度越小。测量模型在SEM的模型中就是一般所谓的验证性因子分析(CFA),用于检验数个测量变量可以构成潜在变量的程度。就潜在变量间关系而言,同时具有外因变量(路径分析的自变量)和内因变量属性(路径分析的因变量)的变量,称为一个中介变量(mediator)。【1】
测量模型分析所验证的属于假设模型内在模型适配度,即模型内在质量的检验,因而测量模型可以检验模型中各因素的收敛效度或聚合效度(convergent validity)与区分效度(discriminant validity)。所谓收敛效度是指测量相同潜在特质的测量指标会落在同一个共同因素上,而区别效度则是指测量不同潜在特质的测量指标会落在不同共同因素上。【1】
2. 结构模型
结构模型又称为因果模型、潜在变量模型(latent variable models)或线性结构关系(linear structrual relationships)。结构方程模型即是潜在变量间因果关系模型的说明,作为因的潜在变量称为外因潜在变量(潜在自变量),作为果的潜在变量称为内因潜在变量(潜在因变量)。在SEM分析模型中,只有测量模型而无结构模型的回归关系,即为验证性因素分析;相反的,只有结构模型而无测量模型,则潜在变量因果关系的探讨,相当于传统的路径分析(path analysis)。结构模型由以下特征:【1】
- 结构方程模型的关系中,单箭头表示变量间的因果关系,双箭头表示两个潜在变量间的相关(共变关系),二者之间无因果关系。
- 变量间关系的建立要有坚强的理论为根据,在既有的解释程度之下,能够以越少的概念和关系来呈现现象的理论越佳。
- 模型界定时必须遵循简约原则,即能以一个比较简单的模型来解释复杂的关系。
(二)结构方程模型的案例
结构方程模型共包括两部分结构,分别是测量关系和影响关系。比如下面这个结构方程模型,其包括四个潜变量,分别是Factor1感知质量、Factor2感知价值、Factor3顾客满意和Factor4顾客忠诚。从测量关系来看:Factor1感知质量由A1~A4共4项测量;Factor2感知价值由B1~B3共3项测量;Factor3顾客满意由C1~C3共3项测量;Factor4顾客忠诚由D1~D2共2项测量。从影响关系来看:Factor1和Factor2对于Factor3产生影响关系;Factor3对Factor4产生影响关系。【3】 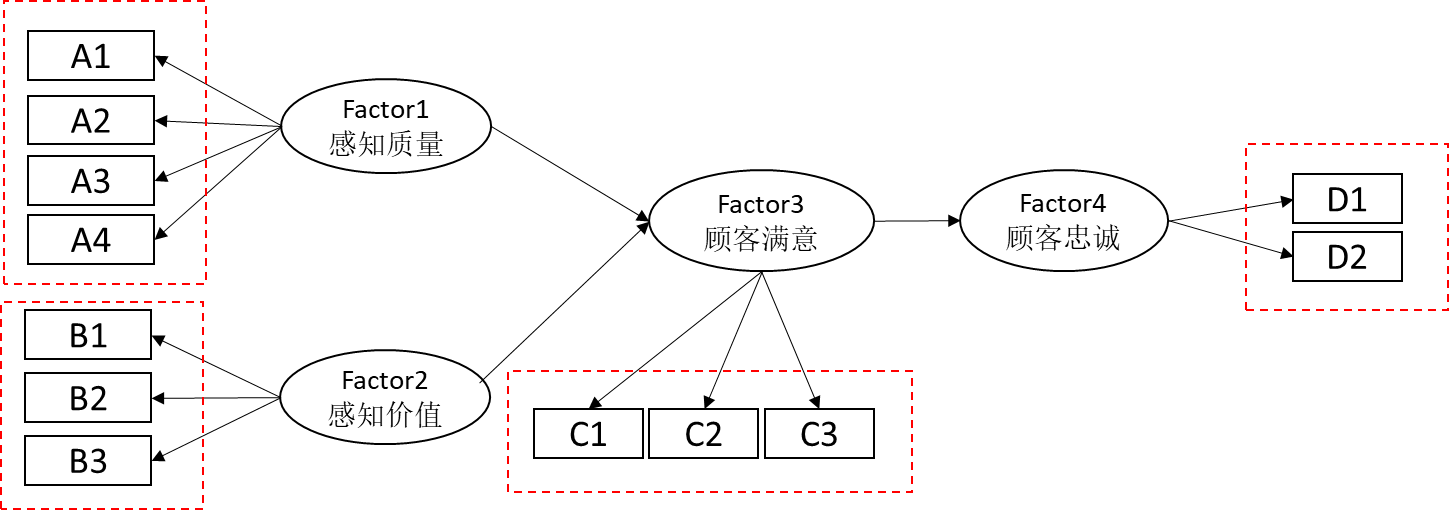
(三)结构方程模型的参数估计方法
1. 样本大小
结构方程模型适用于大样本的分析,取样样本数越大,则统计分析的稳定性与各种指标的适用性也越好。一般而言,大于200以上的样本,才可以称得上是一个中型的样本。有些学者认为,每个观察变量至少10个样本或20个样本。也有研究发现,大部分的结构方程模型研究,其样本数多介于200至500之间。【1】
2. 估计方法
在结构方程模型中,有七种模型估计的方法,其中极大似然法(Maximum Likelihood,ML法)是最广泛应用的估计模型方法,其次是一般化最小平均法(Generalized Least Sqares,GLS法)。极大似然法和一般化最小平均法的基本假定是相同的,包括样本数要够大,观察变量是连续变量,测量指标必须是多变量正态分布,以及必须有效界定模型等。【1】
在估计方法与样本大小的关系方面,极大似然法的样本数量最好大于500,如果样本小于500,则使用一般化最小平均法来估计会获得较佳的结果。如果模型为小样本(60-120),被试人数样本比数据变量的协方差矩阵提供的方差与协方差多,采用渐进分布自由法(Asymptotically distribution-free,ADF法)所获得的估计值较佳。【1】
Amos内设的参数估计方法为极大似然法,但ML法较不适合小样本的估计,对于小样本的SEM分析,Amos另外提供了贝氏估计法(Bayesia estimation)。【1】
(四)模型的概念化与修正
结构方程模型的分析程序有8个步骤:模型的概念化(conceptualization)、路径图(path diagram)的建构、模型的确认(specification)、模型的辨识(identification)、参数估计、模型适配度(model fit)的评估、模型的修改(重新返回到模型的概念化)、模型的复核效化(cross-validation)。【1】
1.模型的概念化
模型的概念化主要是界定潜在变量间的假设关系,以形成作为统计检验的理论框架(theoretical framework)。在结构模型的界定中,研究者必须明确潜在自变量、潜在因变量。其中,一些潜在因变量会直接影响其它的潜在因变量,因而又扮演起自变量的角色,这类潜在因变量称为中介变量。在结构模型概念化中,除了确认这些变量之外,还要注意:因变量的顺序,自变量与因变量、及因变量间的联结关系数目与期望方向,其中变量间期望路径系数的正负号的解释是不相同的。【1】
2. 模型的修正
当模型进行参数估计后,发现假设模型与观察数据的适配度不佳,研究者可能会对模型进行适当修正,修正的目的在于模型适配度的改善。模型的修正如果没有理论基础,完全是数据驱动的,则容易落入“机遇坐大”(capitalization on chance)。模型的修正就是侦测与改正叙列(specification)误差,改善模型适配。所谓叙列误差包括从模型中遗漏了适当的自变量、变量间的重要联结路径,或模型中包含了不适当的联结关系等。【1】
(五)模型适配度的统计量
模型的适配(fit)指的是假设的理论模型与实际数据的一致性程度。在结构方程模型中,所期望获得的结果是“接受虚无假设”,因为不显著的检验结果,表示样本协方差矩阵与假设理论模型隐含的矩阵越接近,表示理论模型越能契合实证数据的结构,模型的适配度越好。假设模型与实际数据是否契合,需要同时考虑三个方面:基本适配指标(preliminary fit criteria)、整体性模型适配度指标(overall model fit)、模型内在结构适配度指标(fit of internal structural model)。【2】1. 模型基本适配指标
在模型基本适配度指标方面,有以下几个准则:【2】
- 估计参数中不能有负的误差方差;
- 所有误差变异必须达到显著水平(t>1.96);
- 估计参数统计量彼此间相关的绝对值不能太接近1(标准化参数系数不能≥1);
- 潜在变量与其测量指标间的因子载荷量,最好介于0.50-0.95之间。
- 不能有很大的标准误。
2. 整体模型适配度指标(模型外在质量的评估)
整体模型的适配度指标又细分为绝对适配指标、相对适配指标以及简约适配指标,具体指标如下:【2】
- X2(卡方值)越小,表示整体模型的因果关系与实际数据越匹配。一个统计不显著(p>0.05)的卡方值,表示接受虚无假设,表示模型的因果路径图模型与实际数据契合。
- χ2 /df <1,表示模型过度适配;>3(较宽松值为5),表示模型适配度不佳;若值介于1-3,表示模型适配度良好。
- SRMR(standardized root mean square residual)为标准化残差均方和平方根,其值介于0-1之间,数值越大表示模型的契合度越差,一般而言模型契合度可以接受的值<0.05。
- RMSEA为渐进残差均方和平方根(root mean square error of approximation)为最重要的适配度指标,RMSEA<0.05,表示模型适配度非常好(good fit);介于0.05-0.08之间,表示模型良好,有合理适配(reasonable fit);在0.08-0.10之间,模型尚可,具有普通适配(modiocre fit);>0.10,表示模型适配欠佳(poor fit)。
- GFI(goodness-of-fit index)为良适性适配指标,GFI介于0-1之间,相当于回归分析中的系数R2,其数值越接近1,表示模型的适配度越好。通常,GFI>0.9,表示模型路径图与实际数据有良好的适配度。
- AGFI(adjusted goodness-of-fit index)为调整后良适性适配指标,类似于调整后R2。AGFI数值也介于0-1之间,当AGFI>0.9,表示模型路径图与实际数据有良好的适配度。
- CFI(comparative fit index)为比较适配指数,属于增值适配度统计(假设模型与基准线模型的适配度比较),介于0(模型完全不适配)和1(模型完全适配)之间。通常CFI>0.9,表示模型路径图与实际数据有良好的适配度。
- 其它增值适配度指标,包括NFI(normed fit index)、RFI(relative fit model)、IFI(incremental fit index)、TLI(tracker-Lewis index)也都类似于CFI,当>0.9时,适配度良好。
3. 模型内在结构适配度的评估(模型内在质量的检验)
内在结构适配的评价包括:(1)测量模型的评价,旨在评估潜在构念的效度和信度;(2)结构模型的评价,旨在评估所理论构建阶段所界定的因果关系是否成立。结构方程模型的适配评估中,测量模型的评估应该先于结构模型的评估。
结构模型适配度的评估包括三个方面:
- 潜在变量间路径系数所代表的参数的符号(正数或负数),是否与原先理论模型所假设的期望的影响方向相同。路径系数为正表示自变量对因变量有正向的影响,为负表示自变量对因变量有负向的影响。
- 假设模型的所有路径系数的参数估计值均必须达到统计显著水平,即|t|>1.96,路径系数达到显著(p<0.05),表示变量间的影响存在实质性意义。
- 多元相关的平方值(R2),越高越好,并且达到显著水平。R2越大,表示因变量被自变量解释的变异量越高。
参考文献
[1] 吴明隆. 结构方程模型——AMOS的操作与应用(第2版)[M].重庆大学出版社,2009.1-33.
[2] 吴明隆. 结构方程模型——AMOS的操作与应用(第2版)[M].重庆大学出版社,2009.37-59.
[3] SPSSAU. 结构方程模型SEM. https://spssau.com/helps/questionnaire/semAnalyse.html